Cosa sono i numeri primi e perché tanto interesse intorno a loro? Un numero n > 0 si definisce primo se è divisibile solo per 1 e per sé stesso con resto 0. L’interesse è dovuto a due motivi, principalmente:
1) I numeri primi sono le basi di tutta l’aritmetica come si può evincere dal Teorema Fondamentale della matematica che recita:“Ogni intero si fattorizza in modo unico come prodotto di numeri primi” e questo li rende indubbiamente affascinanti.
2) I numeri primi molto grandi (ordine di 21024), sono alla base del più utilizzato sistema di crittografia: l’RSA questo invece, attira molto gli esperti in sicurezza informatica…!
Come si trovano i numeri primi?
Fu Eratostene di Cirene (276 – 194 a.c.), il primo a proporre un metodo per “setacciare” i numeri primi, detto appunto: crivello di Eratostene. Esistono diversi algoritmi che risolvono il crivello di Eratostene, questo che propongo mi sembra il più efficiente. Supponiamo dunque di voler trovare tutti i numeri primi da 1 a n, l’algoritmo in pseudocodice è il seguente:
for i := 2 to n-1 do
a[i] := 1
for i := 2 to n-1 do
if a[i]
for j := i to (j*i)<n do
a[i*j] := 0
for i := 2 to n-1 do
if a[i]
print i
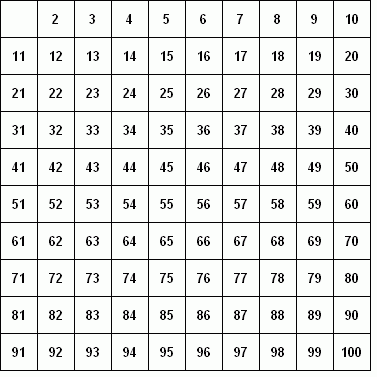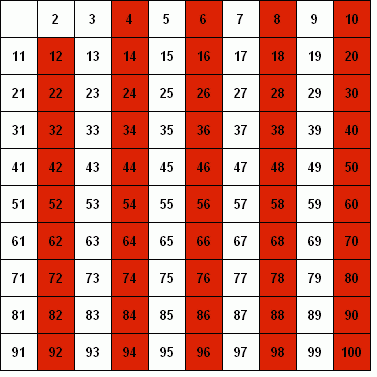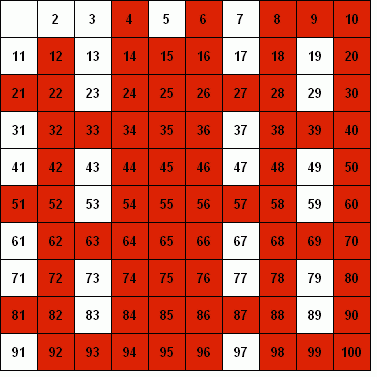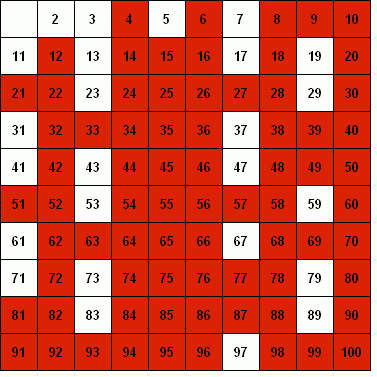
In pratica si procede da i=2 a n, eliminando tutti i multipli di i
(nella immagine in alto a sinistra è possibile vedere un’animazione del processo). Va detto che ancora oggi, pur non essendo l’algoritmo più efficiente in assoluto, è molto utilizzato quando si lavora su numeri relativamente piccoli, per la sua estrema semplicità.
Il metodo della ruota di fattorizzazione (Wheel Factorization)
Già il crivello di Eratostene permette un notevole incremento di prestazioni rispetto ad un processo di “forza bruta” specialmente se l’algoritmo è opportunamente ottimizzato. Il metodo della ruota risulta ancora più efficiente, e vediamo il perché:
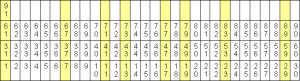
Si scelgono inizialmente come numeri primi di partenza: 2, 3, 5 per ottenere una ruota di lunghezza 30. La lunghezza della ruota è determinta dal prodotto dei numeri primi che decidiamo di utilizzare. Nel nostro caso 2 * 3 * 5 = 30. A questo punto troviamo tutti gli interi che non sono multipli di 2, 3 e 5, il vettore risultate sarà: s[] = {1, 7, 11, 13, 17, 19, 23, 29 }. Abbiamo ottenuto un insieme di numeri che, non sono multipli di 2, 3, 5 e anche se sommati alla lunghezza della ruota o ai suoi multipli (30, 60, 90, ecc), non daranno mai multipli di 2, 3, 5.
Il concetto è più chiaro osservando la figura sotto, le colonne gialle della tabella contengono i soli numeri che andremo a testare, i rimanenenti non sono sicuramente primi, esclusi i numeri di partenza (2, 3, 5). Se provassimo a visualizzare ciascuna riga della tabella come una circonferenza, potremmo immaginare la tabella come una ruota in cui le colonne gialle rappresentano i raggi dove cercare i numeri primi.
Il codice è tratto dall’articolo: “Prime Number Determination Using Wheel Factorization” di rickoshay originariamente scritto in C#, e da me convertito in ANSI C
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 | #include <stdio .h> #include <stdlib .h> unsigned long FirstDivisor(unsigned long candidatePrime); int isPrime(unsigned long primeSuspect); unsigned long FirstDivisor(unsigned long candidatePrime) { const int wheelFactor = 30; int aSieve30[] = {7, 11, 13, 17, 19, 23, 29, 31}; int firstPrimes[] = {2, 3, 5}, i; unsigned long sqrtmax, pass; if (candidatePrime == 1) { return 0; } for (i=0;i<sizeof (firstPrimes)/sizeof(int);i++) { if (candidatePrime % firstPrimes[i] == 0) { return firstPrimes[i]; } } sqrtmax = (unsigned long) sqrt(candidatePrime); for (pass=0; pass<sqrtmax; pass+=wheelFactor) { for (i=0;i<sizeof(aSieve30)/sizeof(int);i++) { if (candidatePrime % (pass + aSieve30[i]) == 0) { return pass + aSieve30[i]; } } } return candidatePrime; } int isPrime(unsigned long primeSuspect) { if (primeSuspect == 0) { return 0; } if (FirstDivisor(primeSuspect) == primeSuspect) { return 1; } else { return 0; } } int main(int argc, char *argv[]) { unsigned long x, i; if (argc == 2) { x = strtoul(argv[1],NULL,10); if (isPrime(x)) { printf("%u e' un numero primo\n",x); } else { printf("%u non e' un numero primo\n",x); } } else { printf ("\nUsage: %s n \nWhere n is an integer number to check for primality\n",argv[0]); } system("PAUSE"); return 0; } |
Download
Il download dell’applicazione (compilata per Win32) è disponibile qui, in formato compresso zip. Sono compresi i sorgenti e i files di progetto per il compilatore DevC++ (ver.: 4.9.9.2). Per l’utilizzo è sufficiente lanciare il programma da una console DOS e passare come parametro il numero da testare.
Conclusioni:
Adottare il metodo della Wheel Factorization per testare la primalità di un numero, consente un incremento di performance pari a (1 – 8 /30) * 100 = 73% con una ruota di dimensioni 30. Le prestazioni possono crescere aumentando le dimensioni della ruota, specialmente quando si ragiona con numeri abbastanza grandi. Il codice proposto utilizza al massimo numeri di 4 byte (unsigned long int = 4,294,967,295) e le performance rimangono accettabili ricompilando per numeri di 8 byte (unsigned long long = 18,446,744,073,709,551,615). In questo caso però sarebbe consigliabile utilizzare una ruota prodotta dai primi 8 numeri primi, come suggerito nell’articolo da cui ho tratto lo spunto per il codice.
Riferimenti ed approfondimenti:
