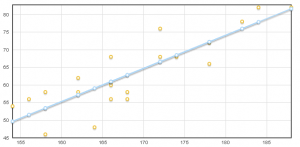
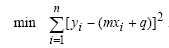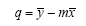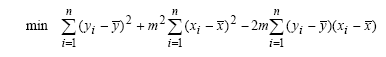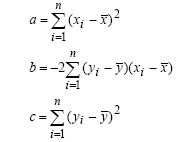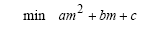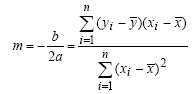statistica

PHP: calcolare la deviazione standard, la varianza, la covarianza e la correlazione

di

Karl PearsonPer rimanere nel tema del precedente post sulla regressione lineare, cioè la statistica, vi propongo una funzione PHP davvero semplicissima che calcola altri quattro fra i più utilizzati indici della cosiddetta “statistica descrittiva”:

1. deviazione standard
2. varianza
3. covarianza
4. correlazione di Pearson

Vediamo brevemente cosa rappresentano e come si calcolano.

Le prime due (deviazione standard e varianza) sono strettamente legate, e servono a fornire la dimensione della dispersione dei dati. Per capire meglio, immaginiamo due serie di dati: a = { 2, 4, 3, 2.5, 3.5, 3 } e b = { 1, 5, 9, -3, -12, 18 }.
In entrambi i casi la media è 3, mentre la deviazione standard di a è = 0.6455 e quella di b è = 9.3986. La deviazione standard ci dice che i dati di b sono molto più dispersi di quelli di a ( …per chi non lo avesse già capito ad occhio!). Bisogna però pensare che la serie potrebbe essere molto lunga e a quel punto il metodo “occhio-metrico”, ovviamente non ci sarebbe di aiuto!

La deviazione standard viene calcolata facendo la radice quadrata della media dei quadrati degli scarti. In effetti elevando al quadrato gli scarti, ci si mette al riparo dalla compensazione che potrebbe essere data dagli scarti positivi e quelli negativi che altrimenti, si annullerebbero

La formula per il calcolo della deviazione standard è:

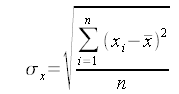
Deviazione standard

La varianza è il quadrato della deviazione standard, e non ci dice nulla di più o di meno…

Formula della varianza:

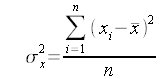
Varianza.png

La covarianza ci indica invece quanto sia contemporanea la variazione di due variabili. E’ interessante notare che, se le due variabili coincidono, ovvero x=y la covarianza diventa la varianza di x.

La formula è:

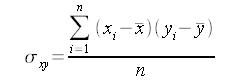
Covarianza.png

I valori che assume la covarianza, non sono troppo leggibili… nel senso che non danno immediatamente il senso della variazione, se non agli addetti ai lavori. In nostro soccorso però, esiste un’altra misura che già dal nome, ci pare di più immediata leggibilità: la correlazione.

Indice di correlazione di Pearson:

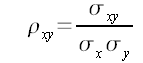
Correlazione

La correlazione di Pearson (nella foto in alto) è il risultato della covarianza diviso il prodotto delle deviazioni standard delle due variabili che si stanno confrontando. Questa misura serve a capire quanto due serie di variabili casuali siano legate fra loro, si dice, appunto: correlate.

Questo coefficiente assume sempre valori compresi fra -1 e +1 e rileggendo le definizioni dei parametri precedenti, è facile capire il perché!

Analizzando il risultato possiamo stabilire che:

  • se ρxy > 0 esiste una correlazione positiva, tanto maggiore quanto ci si avvicina a ρxy = 1
  • se ρxy = 0 non c’è correlazione fra le due variabili, ovvero sono indipendenti
  • se ρxy < 0 esiste una correlazione negativa, tanto maggiore quanto ci si avvicina a ρxy = -1

Sembra piuttosto semplice, ma attenzione alle trappole della statistica: se due variabili danno come risultato del coefficiente di correlazione: 0.87, non è necessariamente detto che abbiano un rapporto di causalità diretto (x dipende da y o viceversa). E’ altrettanto probabile che entrambe dipendano da una terza variabile z che rappresenta una causa comune.

Ed ecco dunque il codice PHP della funzione che restituisce queste misure statistiche. (Ho liberamente tradotto il codice di un programma GW-BASIC scritto da Roberto Vacca e pubblicato sul libro “Anche tu matematico” che è possibile acquistare qui e che consiglio vivamente a tutti di leggere!)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

function correl($X,$Y)
{
  if (!is_array($X) && !is_array($Y)) return false;
  if (count($X) <> count($Y)) return false;
  if (empty($X) || empty($Y)) return false;
 
  $n = count($X);
  $mediaX = array_sum($X)/$n; // media delle x
  $mediaY = array_sum($Y)/$n; // media delle y
 
  $SS = 0;
  $SX = 0;
  $SY = 0;
 
  for($i=0;$i<$n;$i++){
    $SS += ($X[$i] - $mediaX) * ($Y[$i] - $mediaY);
    $SX += pow(($X[$i] - $mediaX),2);
    $SY += pow(($Y[$i] - $mediaY),2);
  }
 
  $M = sqrt($SX)/sqrt($n);
  $M2 = pow($M,2);
  $N = sqrt($SY)/sqrt($n);
  $N2 = pow($N,2);
  $RR = $SS / (sqrt($SX) * sqrt($SY));
 
  $res = array("media x"=>$mediaX, 
               "media y"=>$mediaY,
               "correlazione"=>$RR,
               "varianza x"=>$M2,
               "varianza y"=>$N2,
               "dev. standard x"=>$M,
               "dev. standard y"=>$N
              );
 
  return $res;
}

Conclusioni:

La statistica viene spesso usata per trarre conclusioni tanto categoriche quanto errate. Questo perché a fronte di una certa difficoltà nell’eseguire i calcoli, sembra molto semplice trarre le conclusioni. Ma le cose non stanno proprio così perché, riprendendo appunto una citazione latina dal libro di Roberto Vacca: “Post hoc, ergo propter hoc” (trad.: “dopo di questo, quindi a causa di questo”) è una conclusione semplicistica che non rispecchia quasi mai la realtà, che si presenta spesso decisamente più complessa!

Riferimenti ed approfondimenti:

PHP: calcolare la retta di regressione lineare con i minimi quadrati

di
Grafico della retta di regressione lineare
Grafico della retta di regressione lineare

Uno strumento statistico molto usato in tutti i campi è la regressione lineare con il metodo dei minimi quadrati. Questa procedura serve a trovare una curva che interpoli al meglio una serie di dati campionari, che siano in una certa relazione fra di loro. Esaminiamo il caso più semplice, quello in cui la relazione sia lineare e quindi la migliore curva interpolante sia una retta.
Il metodo dei minimi quadrati si basa sul principio per il quale la migliore curva interpolante di un dato insieme di punti è la curva che ha la proprietà di avere minima la somma degli scarti quadratici, ovvero le differenze elevate al quadrato delle singole distanze fra i punti dati e i punti corrispondenti della retta interpolante.

Il procedimento per determinare i punti della nostra retta viene calcolato risolvendo:

Equazione della retta dei minimi quadrati

sapendo che il termine noto si ricava da:

termine noto della retta dei minimi quadrati

sostituendo q e sviluppando il quadrato si ottiene:

equazione parabola

… a vederla così sembra bruttina, ma con le opportune sostituzioni rispetto a m:

sostituzioni rispetto a m

otteniamo:

equazione parabola semplice

… adesso è più leggibile, è una equazione di una parabola. Trovare il valore minimo equivale a trovare il vertice. Qui bisognerebbe recuperare qualche reminiscenza sul calcolo delle derivate, comunque la soluzione è:

vertice della parabola

m, guarda caso… è anche il coefficiente angolare della nostra retta: quello che ci mancava!
Ora abbiamo in mano tutti i dati per costruire l’algoritmo.
Ecco quindi il codice della funzione, sviluppato in linguaggio PHP:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

function regressione($X,$Y)
{
  if (!is_array($X) &amp;&amp; !is_array($Y)) return false;
  if (count($X) &lt;&gt; count($Y)) return false;
  if (empty($X) || empty($Y)) return false;
 
  $regres = array();
  $n = count($X);
  $mx = array_sum($X)/$n; // media delle x
  $my = array_sum($Y)/$n; // media delle y
  $sxy = 0;
  $sxsqr = 0;
 
  for ($i=0;$i&lt;$n;$i++){
    $sxy += ($X[$i] - $mx) * ($Y[$i] - $my);
    $sxsqr += pow(($X[$i] - $mx),2); // somma degli scarti quadratici medi
  }
 
  $m = $sxy / $sxsqr; // coefficiente angolare
  $q = $my - $m * $mx; // termine noto
 
  for ($i=0;$i&lt;$n;$i++){
    $regres[$i] = $m * $X[$i] + $q;
  }
 
  return $regres;
}

La funzione restituisce l’array delle ordinate della retta di regressione. I dati campione si riferiscono al solito rapporto peso / altezza di alcune persone. Per una più chiara rappresentazione dei dati, è necessario realizzare un grafico con il modello “dispersione” per i dati campionari e il modello “retta” per i dati della regressione.

Ho utilizzato il plugin di JQuery: Flot, facendo generare server-side lo script necessario alla rappresentazione del grafico. L’esempio di applicazione di questa funzione e del grafico correlato è visibile in questa demo.

Per completezza occorre dire che bisognerebbe calcolare anche il coefficiente R2 che fornisce indicazioni sulla qualità della correlazione rispetto ai dati. Il coefficiente varia tra 0 e 1 e, tanto più si avvicina a 1, tanto più i dati sono ben correlati.

Conclusioni:

Un breve ripasso di statistica e matematica delle superiori si è reso necessario per sviluppare un algoritmo molto usato, ma non sempre con cognizione di causa!

Riferimenti ed approfondimenti: