geometria

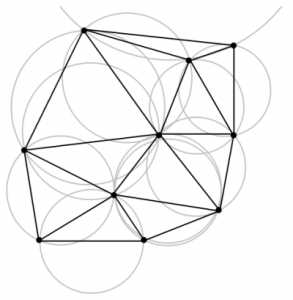
Questa particolare tecnica di Geometria computazionale, che prende il nome dal russo Boris Nikolaevich Delone, francesizzato in Delaunay, consente di definire una griglia di triangoli in una superficie in 2D o in 3D, dato un insieme di punti P.
La griglia viene costruita in modo che, per ogni circonferenza circoscritta ad un triangolo, nessun punto di P (oltre a quelli che formano il triangolo stesso) giace all’interno della circonferenza. Questa condizione viene anche detta di cironferenza libera.

La libreria di funzioni, che propongo è la traduzione “letterale” in PHP delle sole funzioni per superfici in 2D, scritte in codice Visual Basic 6 da Franco Languasco, disponibili qui. Il pacchetto di Languasco è davvero molto ben fatto e contempla anche le funzioni per le triangolazioni in 3D, nonchè la visualizzazione grafica del risultato e la possibilità di ruotare i 3 assi. Il codice iniziale risale in realtà alle librerie GEOMPACK3 di Barry Joe originariamente scritte nel 1991 in linguaggio Fortran.

E’ bene precisare che avendo fatto una traduzione “letterale”, il mio codice PHP non risulta molto elegante, e soprattutto non sfrutta appieno le caratteristiche del linguaggio, sebbene già dai primi test, sembra che le prestazioni siano soddisfacenti!

Esistono diversi algoritmi per le triangolazioni di Delaunay, i più importanti sono:

• Incrementale con complessità O(N2)
• Dividi et impera con complessità O(NlogN)
• Convex Hull con complessità O(NlogN)

L’algoritmo incrementale è quello utilizzato in questa libreria, sebbene non sia chiaramente il più efficiente, va più che bene per un insieme non troppo grande di punti.

Funzionamento:

L’algoritmo incrementale descritto da Dani Lischinski in questo documento, inizia con la costruzione di un primo triangolo, largo a sufficienza per contenere tutti i punti dati. I punti vengono aggiunti uno alla volta verificando che la condizione di circonferenza libera venga rispettata.
La prima operazione è quella di connettere i vertici del triangolo su cui giace il nuovo punto con il punto stesso.

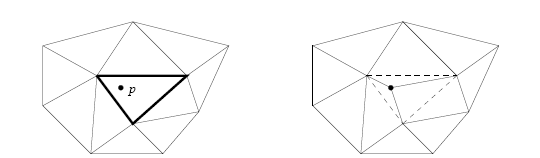
Si vengono così a formare 3 nuovi triangoli. A questo punto i triangoli vengono verificati per la condizione di circonferenza libera.

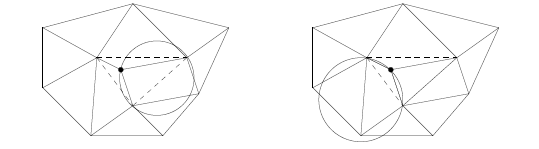
Se è rispettata, si procede con un nuovo punto altrimenti viene eseguita un’operazione che prende il nome di edge flip.

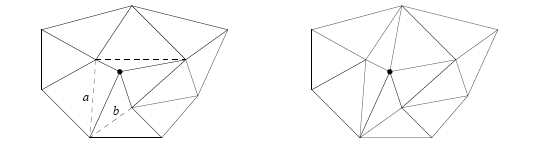
Questa operazione si basa sul concetto che la triangolazione di Delaunay massimizza l’angolo minimo.
Poiché in due triangoli che hanno un lato in comune, la somma degli angoli opposti a tale lato è sempre minore di 180°, sarà sufficiente scambiare le diagonali del quadrilatero formato dai due triangoli come mostrato nella figura sotto.

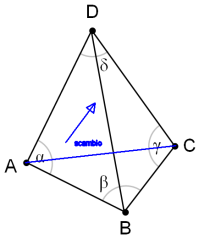
Nel codice della libreria di funzioni, ho volutamente lasciato tutti i commenti originali e ho commentato le istruzioni originali Visual Basic senza cancellarle, per poter controllare meglio eventuali errori di traduzione.
L’intera libreria è visibile qui. Questo, invece, è il codice del file di esempio:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76

<?php 
require_once("delaunay2D.php");
/*
================== PROVA =======================================================
001:   (4.111   0.668)
002:   (-4.209   -3.961)
003:   (-9.720   5.214)
004:   (4.181   -9.093)
005:   (7.252   5.810)
006:   (9.239   7.429)
007:   (8.991   -2.720)
Risultato:
001:   (2   1   3)
002:   (1   2   4)
003:   (1   4   7)
004:   (3   1   5)
005:   (5   1   7)
006:   (3   5   6)
007:   (6   5   7)
*/
//dati
 
  $labels = array("001","002","003","004","005","006","007");
  $XI =  array(4.111,-4.209,-9.720,4.181,7.252,9.239,8.991);
  $YI =  array(0.668,-3.961,5.214,-9.093,5.810,7.429,-2.720); 
 
if (count($XI) <> count($YI)){
  die("le coordinate delle X non sono in numero uguale alle Y");
}
else {
  $NP = count($XI); //N° di punti.  
}
 
echo "Numero punti: ".$NP."<br />";
 
$NT = 0; // N° di triangoli.
 
$IERR = 0;
// Inizializza vettori
$Vcl = array();
$Ind = array();
$TIL = array();
$TNBR = array();
 
    echo ('&lt;pre&gt;');
    for ($I = 1; $I <= $NP; $I++) {
        // Organizza le coordinate dei vertici come
        // richiesto dalle routines di delaunay2D:
        $Vcl[1][$I] = $XI[$I-1]; //Vettore con indice iniziale 1
        $Vcl[2][$I] = $YI[$I-1]; //Vettore con indice iniziale 1
        $Ind[$I] = $I;  // Triangolazione di tutti i vertici contenuti in VCL().
        echo ("Punto $I ".$labels[$I-1]." (".
              $Vcl[1][$I].",".$Vcl[2][$I].")<br />");
    }
    echo ('&lt;/pre&gt;');
 
    // Costruisce le triangolazioni
    $res = DTRIW2($NP, $Vcl, $Ind, $NT, $TIL, $TNBR, $IERR);
 
    echo ("<h2>N. triangoli: ".$NT."</h2>");
 
    if ($IERR == 0) {
      echo ('&lt;pre&gt;');
          for ($I = 1; $I <= $NT; $I++) {
              $Triang[1][$I] = $TIL[1][$I];
              $Triang[2][$I] = $TIL[2][$I];
              $Triang[3][$I] = $TIL[3][$I];
              echo ("Triangolo $I: (".$Triang[1][$I].",".$Triang[2][$I].
                    ",".$Triang[3][$I].")<br />");            
          }
      echo ('&lt;/pre&gt;');        
    }
    else {
      echo "Errore n.: $IERR  - ".zCodiciErrore($IERR)."<br />";
    }
?>

L’array $XI contiene le ascisse dei punti, mentre $YI le ordinate. Tutti i vettori devono avere indice iniziale 1. Le coordinate dei punti vengono passate mediante la matrice $Vcl e il vettore degli indici $Ind alla funzione DTRIW2(). L’output viene fornito passando per riferimento la matrice $TIL così come il vettore per i codici di errore $IERR.

Ho preparato anche questa piccola demo dove è anche possibile visualizzare graficamente i punti su una gif, e al passaggio del mouse, i triangoli che compongono la griglia. Per questo effetto ho utilizzato una map area che viene generata dallo script php e JQuery maphilight uno script che consente di evidenziare le forme geometriche definite nelle map area.

Download

In questo pacchetto è disponibile la libreria e il codice per gli esempi

Ringraziamenti

Ringrazio Franco Languasco per la sua ottima versione Visual Basic 6 senza la quale sarebbe stata dura! Federico Villa, Project Director di Target Tobrukper avermi dato lo spunto a scrivere questo post, e Alessandro Scoscia per le sue dritte geniali!

Conclusioni

Non ho trovato molto sulla generazione di griglie di superfici 2D utilizzando il metodo di Delaunay in PHP, questo potrebbe essere un inizio. Spero, in futuro di migliorare il “porting”, al momento piuttosto grezzo, di questa libreria. Infine, una raccomandazione: non ho potuto testare in modo esaustivo il codice, quindi prima di utilizzarla è bene fare un po’ di prove. Fatemi sapere, in caso di errori!

Riferimenti ed approfondimenti:

• Wikipedia: Delaunay triangulation (in english)
• GEOMPACK3 – 2D, 3D and KD Computational Geometry (in english)
• Stefano Rebay: Triangolazione di Delaunay – Dipartimento di Ingegneria Meccanica Università di Brescia (pdf)
• Elementi di Geometria Computazionale (pdf)
• Algoritmi per la triangolazione di Delaunay (pdf)
• Delaunay Triangulation Algorithms (java applet)

Questa classe PHP determina se un certo punto di coordinate P(x,y) si trova all’interno di un poligono convesso oppure no. Inoltre calcola la lunghezza di ciascun lato, il perimetro, l’area, e l’ampiezza di ciascun angolo.Può essere applicata a qualsiasi poligono convesso di cui si abbiano le coordinate cartesiane dei vertici in 2D. Le coordinate dei vertici verranno fornite in stretta successione, non importa se in senso orario o antiorario, in un array multidimensionale. E’ stato scelto di considerare solo poligoni convessi, per semplificare il calcolo degli angoli interni che risulteranno tutti < di 180°. La condizione che il poligono fornito sia convesso viene controllata verificando che il segno di ogni lato con il vertice successivo non cambi. Con lo stesso metodo viene verificato se un punto dato si trova all’interno o all’esterno del poligono. Infine, per semplificare, ho considerato che se il punto giace su uno dei lati, viene considerato interno.
La classe è compatibile con PHP 4.

Funzionamento:

Dati due punti A(x0,y0); e B(x1,y1), possiamo definire l’equazione canonica della retta passante per i due punti come:
x (y0 − y1) - y (x0 − x1) + x0 y1 - x1 y0 = 0
Il polinomio che è rappresentato dal primo membro dell’equazione, sarà = 0 nel caso di un punto sulla retta, produrrà valori positivi se si trova su un lato e negativi se si trova sul lato opposto.
E’ dunque chiaro che per verificare se un punto si trova all’interno del poligono è sufficiente confrontare il segno che assume l’equazione, sostituendo ad x e y le coordinate del punto, rispetto ad ogni lato. Se il segno cambia, si trova all’esterno.
Poiché ho imposto che il poligono sia convesso, ho potuto ridurre l’algoritmo confrontando il risultato del segno fra ogni lato e il punto dato, solo con il segno del primo lato e il vertice successivo (nei poligoni convessi ogni lato “gira” dalla stessa parte).

Il calcolo della misura di ciascun lato viene fatto usando la formula della distanza fra due punti:

Si intendono p(px,py) e q(qx,qy) due vertici del poligono.

Il calcolo della misura di ciascun angolo viene fatto usando la formula del coseno:

a2 = b2 + c2 - 2 bc cos α

In cui α è l’angolo compreso fra b e c.

L’area viene calcolata usando la formula Shoelace:

Considerando che: (x_{n + 1}; y_{n + 1}) = (x₁; y₁).

Ecco il codice:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149

<?php
class ConvexPolygon2D
{
  var $EPSILON = 0.000001;
  var $points = array();
  var $polySides = array();
  var $polyAngles = array();
  var $nVertex = 0;
  var $polySign = 0;
 
  function ConvexPolygon2D($points)
  {
    $this->points = $points;
    $this->nVertex = count($points);
    $this->polySign = $this->sign($points[0],$points[1],$points[2]);
    if (!$this->isConvexHull()) die ("This polygon is not convex!"); 
    $this->sides();
    $this->angles();
  }  
 
  function sign ($a, $b, $p)
  {
    $c = $p[0] * ($a[1] - $b[1]) - $p[1] * ($a[0] - $b[0]) + 
         $a[0] * $b[1] - $a[1] *$b[0];
    if (abs($c)< $EPSILON)    
    {
      return 0;
    }
    elseif ($c > 0)
    {
      return 1;
    }
    else
    {
      return -1;
    }
  }
 
  function isConvexHull()
  {
    for ($i=0; $i<$this->nVertex-1; $i++)
    {
      $lastVertex = $i+2;
      if ($lastVertex>=$this->nVertex)
         $lastVertex = 0;
      $psign = $this->polySign * 
               $this->sign($this->points[$i],
               $this->points[$i+1],
               $this->points[$lastVertex]);
      if($psign==0) die ("Two sides on the same line!"); 
      if ($psign<0)
      {
        return false;
      }
 
    }
    return true;
  }
 
  function isInConvexHull ($p)
  {
    for ($i=0; $i<=$this->nVertex-1; $i++)
    {
      $lastVertex = $i+1;
      if ($lastVertex>=$this->nVertex)
         $lastVertex = 0;
         $psign = $this->polySign * 
                $this->sign($this->points[$i],$this->points[$lastVertex],$p);
 
      if ($psign<0)
      {
        return false;
      }
 
    }
    return true;
  }  
 
  function RadToDeg($radians)
  {
    return $radians * 180 / M_PI;
  }
 
  function vertexDist($a,$b)
  {
    return sqrt(pow(($b[0]-$a[0]),2)+pow(($b[1]-$a[1]),2));
  }
 
  function perimeter()
  {
    return array_sum($this->polySides);
  }
 
 
  function sides()
  {
    for ($i=0; $i<$this->nVertex; $i++)    
    {
      $lastVertex = $i+1;
      if ($lastVertex>=$this->nVertex)
         $lastVertex = 0;
      $this->polySides[] = $this->vertexDist($this->points[$i],
                           $this->points[$lastVertex]);
    }
    return true; 
  }
 
  function angles()
  {
    for ($i=0; $i<$this->nVertex; $i++)    
    {
      $this->polyAngles[] = $this->angle($i);
    }
    return true;    
  }
 
  function angle($vertex)
  {
    //Teorema del coseno: a² = b² + c² - 2bc cosα
    $a = empty($vertex) ? $this->vertexDist($this->points[$this->nVertex-1],
        $this->points[1]) : 
        ($vertex==$this->nVertex-1 ? $this->vertexDist($this->points[$vertex-1],
        $this->points[0]) : $this->vertexDist($this->points[$vertex-1],
        $this->points[$vertex+1]));
 
    $b = $this->polySides[$vertex];
    $c = empty($vertex) ? $this->polySides[$this->nVertex-1] : 
        $this->polySides[$vertex-1];
 
    $res = (pow($b,2) + pow($c,2) - pow($a,2)) / (2 * $b * $c);
    return $this->RadToDeg(acos($res));
  }
 
  function area()
  {
    //Calcolo dell'area con la Shoelace formula.
    $dArea = 0;
    for ($i=0; $i<$this->nVertex; $i++)    
    {
      $lastVertex = $i+1;
      if ($lastVertex>=$this->nVertex)
         $lastVertex = 0;
      $dArea += ($this->points[$i][0]*$this->points[$lastVertex][1]) - 
                ($this->points[$lastVertex][0]*$this->points[$i][1]);
    }
    return abs($dArea) /2;  
  }
}
?>

Un esempio del funzionamento della classe è visibile qui. Per rendere graficamente le figure dei poligoni e dei punti ho utilizzato le librerie JavaScript VectorGraphics di Walter Zorn. E’ necessario, quindi, che Javascript sia attivo nel browser.

Nota: le librerie grafiche utilizzano <div>; di tipo canvas, e con Internet Explorer, alcune figure vengono disegnate in modo non perfetto, mentre con Mozilla non ci sono problemi

Il pacchetto completo è scaricabile qui

Riferimenti ed approfondimenti:

• NUMERI e ALGORITMI. Dentro o fuori il triangolo? (pdf)
• Determining if a point lies on the interior of a polygon (in english)
• PNPOLY – Point Inclusion in Polygon Test (in english)
• Wikipedia: Poligono
• Wikipedia: Teorema del coseno
• Charles L. Hamberg and Ronald Vavrinek: SHOELACE ALGORITHM (pdf in english)