id = 4, e parentId = 1, l’elemento 9 avrà id = 9, e parentId = 4, e così via. Questo modello offre alcuni vantaggi, che sono principalmente la semplicità della struttura e la velocità negli inserimenti. D’altro canto, risultano piuttosto onerosi processi come l’estrazione o la cancellazione di interi rami. Le query risultano quindi, complesse e spesso ricorsive.
Sebbene l’utilizzo di una struttura di tipo nested tree model ideata da Joe Celko sia quasi sempre preferibile, alle volte è necessario cimentarsi con gli algoritmi per la manipolazione delle liste di adiacenza.
Se si deve salire da una foglia fino alla root, non è troppo difficile, basta risalire, attraverso il parentId, il genitore finché parentId = NULL. Il procedimento naturalmente ricorsivo, per questo motivo spesso si indica l’attributo parentId anche con il nome di ricorsore.
Il gioco si fa duro quando si deve estrarre un ramo a partire da un certo genitore… ma come disse John Belushi: “When the going gets tough, the toughs get going!”. Vediamo come fare evitando di farci del male con stored procedure, query ricorsive o tabelle temporanee.
La soluzione che ho adottato prende spunto dagli algoritmi di attraversamento dei grafi: Breadth-first search e Depth-first search. Questi sono procedimenti non ricorsivi che utilizzano stack di tipo FIFO e LIFO per l’esplorazione dei nodi.
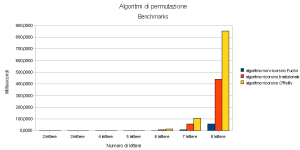
L’operazione di fetching da un archivio che rappresenta l’albero della figura in alto produrrà un’array di questo tipo:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | $arrTest = array ( 0 => array ("id"=>1, "parent_id"=>NULL), 1 => array ("id"=>2, "parent_id"=>1), 2 => array ("id"=>3, "parent_id"=>1), 3 => array ("id"=>4, "parent_id"=>1), 4 => array ("id"=>5, "parent_id"=>2), 5 => array ("id"=>6, "parent_id"=>2), 6 => array ("id"=>7, "parent_id"=>3), 7 => array ("id"=>8, "parent_id"=>3), 8 => array ("id"=>9, "parent_id"=>4), 9 => array ("id"=>10, "parent_id"=>4), 10 => array ("id"=>11, "parent_id"=>4), 11 => array ("id"=>12, "parent_id"=>5), 12 => array ("id"=>13, "parent_id"=>5), 13 => array ("id"=>14, "parent_id"=>6), 14 => array ("id"=>15, "parent_id"=>7), 15 => array ("id"=>16, "parent_id"=>7), 16 => array ("id"=>17, "parent_id"=>9), 17 => array ("id"=>18, "parent_id"=>9), 18 => array ("id"=>19, "parent_id"=>10), 19 => array ("id"=>20, "parent_id"=>11), 20 => array ("id"=>21, "parent_id"=>11) ); |
Ammettiamo ora di voler estrarre l’intero ramo che ha come radice l’elemento 4. La funzione seguente utilizza un nuovo array che viene costruito utilizzando come chiave gli id e come valori i parent_id. Questo ci permette di utilizzare la funzione PHP: array_keys() per le ricerche dei figli, che è piuttosto efficiente.
Ecco il codice:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | function getBranch ($arr,$pk,$recursor,$idBranch) { $pksArr = array(); foreach ($arr as $rec) { $pksArr[$rec[$pk]]=$rec[$recursor]; } $branchIds = array($idBranch); $i=0; while ($i<count($branchIds)) { $newKeys = array_keys($pksArr,$branchIds[$i]); if (!empty($newKeys)) { foreach ($newKeys as $newKey){ array_push($branchIds, $newKey); } } ++$i; } $res = array(); foreach ($arr as $child) { if (in_array($child[$pk], $branchIds)) { $res[] = $child; } } return $res; } |
Certo, il codice di questa funzione non è troppo ottimizzato: utilizza tre array (anche se $pksArr e $branchIds sono monodimensionali e quindi “leggeri”) ed esegue tre cicli. In particolare il ciclo (righe 19-23) è piuttosto lento, ma è necessario se si vuole recuperare tutti gli attributi degli elementi estratti oltre agli indispensabili id già presenti in $branchIds. Dalle prove che ho fatto, per archivi fino a 10-15000 records risulta comunque abbastanza efficiente.
Questo è il risultato dell’estrazione del ramo con radice 4 (si nota che l’andamento è di tipo “breadth-first-search” ricerca in ampiezza, seguendo i colori: rosso-verde-blu-giallo):
Array
(
[0] => Array
(
[id] => 4
[parent_id] => 1
)
[1] => Array
(
[id] => 9
[parent_id] => 4
)
[2] => Array
(
[id] => 10
[parent_id] => 4
)
[3] => Array
(
[id] => 11
[parent_id] => 4
)
[4] => Array
(
[id] => 17
[parent_id] => 9
)
[5] => Array
(
[id] => 18
[parent_id] => 9
)
[6] => Array
(
[id] => 19
[parent_id] => 10
)
[7] => Array
(
[id] => 20
[parent_id] => 11
)
[8] => Array
(
[id] => 21
[parent_id] => 11
)
)
// Tempo di esecuzione: 0.2388 msecs
Conclusioni
Personalmente, ho una certa ritrosia nell’uso di funzioni ricorsive, per questo ho perso del tempo a cercare soluzioni alternative e cicliche, ciò non toglie che, ad esempio per recuperare il percorso di una foglia (risalendo quindi verso la root), la ricorsione sia la soluzione più adatta.
Riferimenti ed approfondimenti: