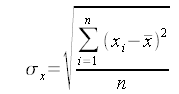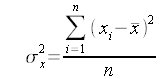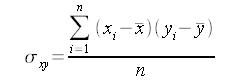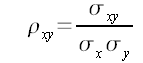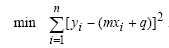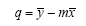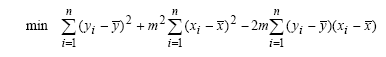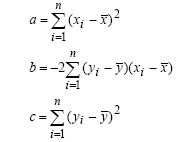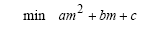 Questa classe PHP determina se un certo punto di coordinate P(x,y) si trova all’interno di un poligono convesso oppure no. Inoltre calcola la lunghezza di ciascun lato, il perimetro, l’area, e l’ampiezza di ciascun angolo.Può essere applicata a qualsiasi poligono convesso di cui si abbiano le coordinate cartesiane dei vertici in 2D. Le coordinate dei vertici verranno fornite in stretta successione, non importa se in senso orario o antiorario, in un array multidimensionale. E’ stato scelto di considerare solo poligoni convessi, per semplificare il calcolo degli angoli interni che risulteranno tutti < di 180°. La condizione che il poligono fornito sia convesso viene controllata verificando che il segno di ogni lato con il vertice successivo non cambi. Con lo stesso metodo viene verificato se un punto dato si trova all’interno o all’esterno del poligono. Infine, per semplificare, ho considerato che se il punto giace su uno dei lati, viene considerato interno.
Questa classe PHP determina se un certo punto di coordinate P(x,y) si trova all’interno di un poligono convesso oppure no. Inoltre calcola la lunghezza di ciascun lato, il perimetro, l’area, e l’ampiezza di ciascun angolo.Può essere applicata a qualsiasi poligono convesso di cui si abbiano le coordinate cartesiane dei vertici in 2D. Le coordinate dei vertici verranno fornite in stretta successione, non importa se in senso orario o antiorario, in un array multidimensionale. E’ stato scelto di considerare solo poligoni convessi, per semplificare il calcolo degli angoli interni che risulteranno tutti < di 180°. La condizione che il poligono fornito sia convesso viene controllata verificando che il segno di ogni lato con il vertice successivo non cambi. Con lo stesso metodo viene verificato se un punto dato si trova all’interno o all’esterno del poligono. Infine, per semplificare, ho considerato che se il punto giace su uno dei lati, viene considerato interno.
La classe è compatibile con PHP 4.
Funzionamento:
Dati due punti A(x0,y0); e B(x1,y1), possiamo definire l’equazione canonica della retta passante per i due punti come:
x (y0 − y1) - y (x0 − x1) + x0 y1 - x1 y0 = 0
Il polinomio che è rappresentato dal primo membro dell’equazione, sarà = 0 nel caso di un punto sulla retta, produrrà valori positivi se si trova su un lato e negativi se si trova sul lato opposto.
E’ dunque chiaro che per verificare se un punto si trova all’interno del poligono è sufficiente confrontare il segno che assume l’equazione, sostituendo ad x e y le coordinate del punto, rispetto ad ogni lato. Se il segno cambia, si trova all’esterno.
Poiché ho imposto che il poligono sia convesso, ho potuto ridurre l’algoritmo confrontando il risultato del segno fra ogni lato e il punto dato, solo con il segno del primo lato e il vertice successivo (nei poligoni convessi ogni lato “gira” dalla stessa parte).
Il calcolo della misura di ciascun lato viene fatto usando la formula della distanza fra due punti:
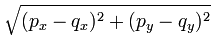
Si intendono p(px,py) e q(qx,qy) due vertici del poligono.
Il calcolo della misura di ciascun angolo viene fatto usando la formula del coseno:
a2 = b2 + c2 - 2 bc cos α
In cui α è l’angolo compreso fra b e c.
L’area viene calcolata usando la formula Shoelace:
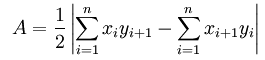
Considerando che: (xn + 1; yn + 1) = (x1; y1).
Ecco il codice:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 | <?php class ConvexPolygon2D { var $EPSILON = 0.000001; var $points = array(); var $polySides = array(); var $polyAngles = array(); var $nVertex = 0; var $polySign = 0; function ConvexPolygon2D($points) { $this->points = $points; $this->nVertex = count($points); $this->polySign = $this->sign($points[0],$points[1],$points[2]); if (!$this->isConvexHull()) die ("This polygon is not convex!"); $this->sides(); $this->angles(); } function sign ($a, $b, $p) { $c = $p[0] * ($a[1] - $b[1]) - $p[1] * ($a[0] - $b[0]) + $a[0] * $b[1] - $a[1] *$b[0]; if (abs($c)< $EPSILON) { return 0; } elseif ($c > 0) { return 1; } else { return -1; } } function isConvexHull() { for ($i=0; $i<$this->nVertex-1; $i++) { $lastVertex = $i+2; if ($lastVertex>=$this->nVertex) $lastVertex = 0; $psign = $this->polySign * $this->sign($this->points[$i], $this->points[$i+1], $this->points[$lastVertex]); if($psign==0) die ("Two sides on the same line!"); if ($psign<0) { return false; } } return true; } function isInConvexHull ($p) { for ($i=0; $i<=$this->nVertex-1; $i++) { $lastVertex = $i+1; if ($lastVertex>=$this->nVertex) $lastVertex = 0; $psign = $this->polySign * $this->sign($this->points[$i],$this->points[$lastVertex],$p); if ($psign<0) { return false; } } return true; } function RadToDeg($radians) { return $radians * 180 / M_PI; } function vertexDist($a,$b) { return sqrt(pow(($b[0]-$a[0]),2)+pow(($b[1]-$a[1]),2)); } function perimeter() { return array_sum($this->polySides); } function sides() { for ($i=0; $i<$this->nVertex; $i++) { $lastVertex = $i+1; if ($lastVertex>=$this->nVertex) $lastVertex = 0; $this->polySides[] = $this->vertexDist($this->points[$i], $this->points[$lastVertex]); } return true; } function angles() { for ($i=0; $i<$this->nVertex; $i++) { $this->polyAngles[] = $this->angle($i); } return true; } function angle($vertex) { //Teorema del coseno: a² = b² + c² - 2bc cosα $a = empty($vertex) ? $this->vertexDist($this->points[$this->nVertex-1], $this->points[1]) : ($vertex==$this->nVertex-1 ? $this->vertexDist($this->points[$vertex-1], $this->points[0]) : $this->vertexDist($this->points[$vertex-1], $this->points[$vertex+1])); $b = $this->polySides[$vertex]; $c = empty($vertex) ? $this->polySides[$this->nVertex-1] : $this->polySides[$vertex-1]; $res = (pow($b,2) + pow($c,2) - pow($a,2)) / (2 * $b * $c); return $this->RadToDeg(acos($res)); } function area() { //Calcolo dell'area con la Shoelace formula. $dArea = 0; for ($i=0; $i<$this->nVertex; $i++) { $lastVertex = $i+1; if ($lastVertex>=$this->nVertex) $lastVertex = 0; $dArea += ($this->points[$i][0]*$this->points[$lastVertex][1]) - ($this->points[$lastVertex][0]*$this->points[$i][1]); } return abs($dArea) /2; } } ?> |
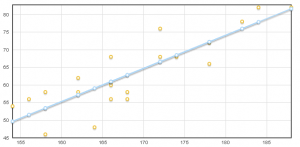
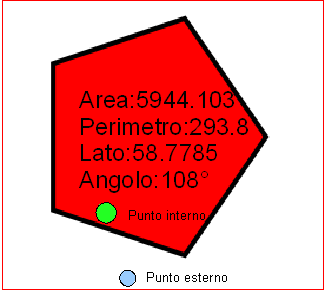
Un esempio del funzionamento della classe è visibile qui. Per rendere graficamente le figure dei poligoni e dei punti ho utilizzato le librerie JavaScript VectorGraphics di Walter Zorn. E’ necessario, quindi, che Javascript sia attivo nel browser.
Nota: le librerie grafiche utilizzano <div>; di tipo canvas, e con Internet Explorer, alcune figure vengono disegnate in modo non perfetto, mentre con Mozilla non ci sono problemi
Il pacchetto completo è scaricabile qui
Riferimenti ed approfondimenti: