distanze euclidee

PHP: una classe per il calcolo di matrici di distanze euclidee, cityblock e Minkowski

di

EuclideSono diversi gli ambiti nei quali può essere necessario raggruppare elementi di un certo insieme in base a differenze registrate attraverso misure sul campo. In questi casi per la determinazione dell’entità delle differenze, viene usata la distanza che può essere considerata al di là del suo significato metrico, una misura della diversità. I campi di applicazione possono essere i più disparati: dagli aspetti biologici come per esempio differenze genotipiche o fenotipiche di individui o popolazioni, agli aspetti socio-economici come redditi, produttività o consumo.
Non tutte le variabili, però, possono essere trattate allo stesso modo. Solo le variabili che vengono definite “ad intervallo”, possono essere utilizzate per calcolare distanze di tipo metrico come le distanze euclidee, city-block (o Manhattan) e di Minkowski. Parliamo quindi di variabili quantitative. Negli altri casi, a seconda del tipo di variabile utilizzato (dicotomiche, categoriali, ecc) le differenze possono essere comunque calcolate mediante l’utilizzo di distanze non metriche o ultra-metriche.
A questo punto è bene definire cosa sono le distanze metriche. Sono quelle che rispettano i seguenti enunciati:

  • la distanza tra due punti che non coincidono deve essere positiva;
  • la distanza tra due punti che coincidono è pari a 0;
  • la distanza tra due punti deve essere simmetrica (d AB = d BA),

e non contravvengono la proprietà della disuguaglianza triangolare, cioè dati tre punti A, B e C deve essere verificata la condizione che:
d AB < d AC + d BC
riassumendo, si può dire che sono quelle che seguono la metrica pitagorica.

Fatta questa doverosa premessa, passiamo ad analizzare le formule delle distanze metriche utilizzate
nella classe PHP.

Distanze Euclidee

E’ senza dubbio il tipo di distanza più diffuso. La formula per il calcolo deriva dalla formula della distanza fra 2 punti in un piano cartesiano e può essere espressa come:

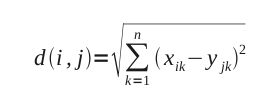
Formula per il calcolo delle distanze euclidee

in cui xik e xjk sono le misure in posizione i e j rispettivamente della k-esima di n variabili.

Distanze city-block (Manhattan)

Viene anche detta distanza assoluta o della metrica del taxi. La sua formula è:

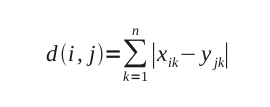
Formula per il calcolo delle distanze city-block

La particolarità di questa formula sta nel fatto che, considerando la distanza euclidea fra 2 punti A e C di un triangolo ABC, e che questa distanza può essere espressa come la radice quadrata della somma dei quadrati costruiti sui cateti del triangolo ABC, la distanza di city-block è la somma dei cateti di questo triangolo. Il concetto risulta forse più chiaro osservando la figura qui sotto.

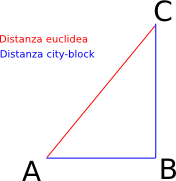
Triangolo di esempio

Non a caso, il nome Manhattan deriva proprio dalla particolare disposizione delle strade del famoso quartiere di New York, che si incrociano ad angolo retto, formando una sorta di scacchiera. In effetti questo tipo di distanza, ben si presta a rappresentare il percorso reale fra due punti che si trovano in prossimità degli angoli opposti di un palazzo (…o grattacielo!)

Distanze di Minkowski

Rappresenta la forma più generalizzata di distanza metrica. La sua formula è:

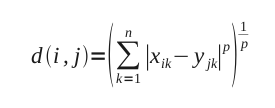
Formula per il calcolo delle di minkowski

Si dice di ordine p, e in particolare quando p=1, coincide con la distanza city-block,
e quando p=2, coincide con la distanza euclidea, come si evince dalla formula. Per p -> infinito coincide con la distanza di Lagrange o di Chebychev.

La classe PHP che ho preparato permette di calcolare, scegliendo una delle distanze illustrate sopra, una matrice triangolare (nella quale la diagonale assume valori = 0) di confronto fra tutti i campioni passati in input. La matrice dati da passare come parametro al costruttore deve avere questo formato:

1
2
3
4
5
6
7
8
9
10
11
12

$dataTest = array (
                "sample01" => array(82.897,488,0.6381,8.576),
                "sample02" => array(37.04,512,0.7935,7.9293),
                "sample03" => array(86.571,617,0.1518,0.9705),
                "sample04" => array(76.038,876,0.0883,5.5867),
                "sample05" => array(67.726,687,0.9145,9.2478),
                "sample06" => array(34.407,979,0.8148,3.8348),
                "sample07" => array(52.258,462,0.7132,3.716),
                "sample08" => array(75.141,652,0.8453,8.3466),
                "sample09" => array(17.546,322,0.0483,1.5812),
                "sample10" => array(35.786,502,0.6899,3.1447)
                );

Ed ecco dunque il codice PHP della classe:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84

class DistanceMatrix
{
 var $dataArray = null;
 var $dataSize = 0;
 var $dataVectSize = 0;
 
 function DistanceMatrix($data)
 {
  $this->dataArray = array();
  $this->dataArray = $data;
  $this->checkData();
 }
 
 function checkData()
 {
  $this->dataSize = count($this->dataArray);
  if($this->dataSize < 2){
   die("Cannot proceed: only one sample, or missing data");
  }
  reset ($this->dataArray);
  $this->dataVectSize = count(current($this->dataArray));
  foreach ($this->dataArray as $key => $vectData){
   $vectSize = count($vectData);
   if ($vectSize != $this->dataVectSize){
    die("Cannot proceed: different size vectors!");
   }
  }
 }
 
 function euclidean ($vect1,$vect2)
 {
  $qdist = 0.0;
  for($i=0;$i< $this->dataVectSize;$i++){
   $qdist += pow($vect1[$i]-$vect2[$i],2);
  }
  return sqrt($qdist);
 }
 
 function manhattan ($vect1,$vect2)
 {
  $dist = 0.0;
  for($i=0;$i< $this->dataVectSize;$i++){
   $dist += abs($vect1[$i]-$vect2[$i]);
  }
  return $dist;
 }
 
 function minkowski($vect1,$vect2,$exp) {
  $edist = 0.0;
  for($i=0; $i< $this->dataVectSize; $i++){
   $edist += pow(abs($vect1[$i]-$vect2[$i]), $exp);
  }
  return pow($edist, 1/$exp);
 }
 
 function printData($distType,$exp=1)
 {
  if (!method_exists($this,$distType)) {
   die ("Sorry, can't find $distType method!");
  }
  echo ("<h1>Matrix of $distType distances </h1>\n");
  echo ("<table class='datatable' summary='Results'>\n");
  echo ("<thead><tr>");
  echo ("<th>&nbsp;</th>");
  foreach ($this->dataArray as $key=>$data){
   echo ("<th>".$key."</th>");
  }
  echo ("</tr></thead><tbody>\n");
  foreach ($this->dataArray as $keyA=>$dataA){
   echo ("<tr>");
   echo ("<td><strong>".$keyA."</strong></td>");
   foreach ($this->dataArray as $keyB=>$dataB){
    if ($distType=="minkowski"){
     printf("<td>%.4f</td>",$this->minkowski($dataA,$dataB,$exp));
    }
    else{
     printf("<td>%.4f</td>",$this->$distType($dataA,$dataB));
    }
   }
   echo ("</tr>\n");
  }
  echo ("</tbody></table>\n");
 }
}

Demo:

In questa pagina è visibile una demo della classe con dei campioni ipotetici e delle variabili di test.

Download

Il download della classe completa del file di esempio è disponibile qui.

Conclusioni:

La naturale conclusione della produzione di una matrice di distanze è l’elaborazione di una cluster analisys. Questo metodo permette di leggere visivamente i raggruppamenti dovuti alle similarità o diseguaglianze indicate dalle distanze calcolate. Tali raggruppamenti potranno essere espressi in forma gerarchica. Un software distribuito con licenza GNU che permette queste elaborazioni, e che suggerisco
è Cluster 3.0, disponibile per Linux, Windows e MacOSX.

Riferimenti ed approfondimenti: