matematica

PHP: Quando Tartaglia e Fibonacci si davano la mano

di

Tartaglia e FibonacciDi certo, in vita i due non si sarebbero mai potuti dare la mano, essendo vissuti in epoche distanti ben tre secoli. Fibonacci, al secolo Leonardo Pisano, visse infatti a cavallo del 1200 ed era di famiglia benestante essendo il padre (Bonaccio, da qui il nome FiBonacci) il segretario della Repubblica di Pisa e responsabile del commercio con l’Africa. Fu proprio in Africa che ebbe modo di studiare le avanzate tecniche matematiche, al tempo in possesso del mondo arabo.
Tartaglia, al secolo Niccolò Fontana visse a cavallo del 1500 fra Brescia e Verona. Era di famiglia tutt’altro che ricca, e rimase orfano di padre quando era ancora molto giovane. Ebbe anche la disgrazia di rimanere sfregiato durante il sacco di Brescia del 1512 ad opera dell’esercito francese. A leggere il suo stesso racconto c’è da stupirsi di come sia riuscito a sopravvivere a ferite così gravi. Rimase diversi giorni senza poter parlare e mangiare cibi solidi proprio a causa dei colpi di spada inferti sulla sua testa, e quando guarì non riuscì più a parlare senza balbettare, da questo il suo soprannome Tartaglia con il quale divenne famoso.

Il triangolo di Tartaglia

Tutti noi ricordiamo, dai tempi delle superiori, la piramide di numeri che compongono il famoso triangolo di Tartaglia, e lo ricordiamo soprattutto in relazione allo studio delle potenze di un binomio.

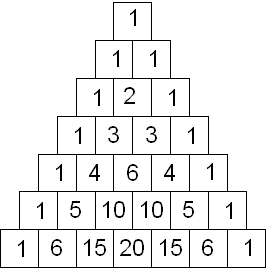
Triangolo di Tartaglia

Ogni riga, riporta i coefficienti dell’espansione del binomio con esponente uguale al numero di riga – 1 (iniziando a contare dal vertice della piramide) Così ad esempio, per esponente 3 avremo:
(a + b)3 = 1a3 + 3a2b + 3ab2 + 1b3

La successione di Fibonacci

La successione dei numeri di Fibonacci è nota soprattutto per la particolarità che il rapporto tra un numero e quello precedente, man mano che si procede nella successione, tende alla sezione aurea La successione fu trovata da Fibonacci, rispondendo al quesito: “Supponiamo di avere una coppia di conigli, che dopo un mese è in grado di generare una seconda coppia di conigli, quante coppie avremo in un anno?” (Ammesso che ogni coppia generi sempre e solo una coppia al mese e nessuno muoia…). Il procedimento è molto semplice: ogni numero, ad eccezione dei primi due (1, 1), è la somma dei due che lo precedono. Quindi:
F(12) = 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144

Dove si incontrano Tartaglia e Fibonacci?

Per capire il punto di contatto fra i due, è necessario modificare la forma del triangolo di Tartaglia, disponendo i numeri nelle celle che costituiscono un triangolo rettangolo piuttosto che isoscele, in questo modo:

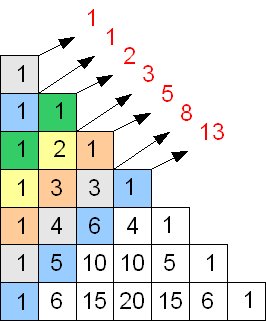
Triangolo di Tartaglia

I numeri che costituiscono le diagonali ascendenti di questa matrice triangolare, sommati fra loro, generano la successione di Fibonacci.

Ecco dunque una classe PHP che calcola i valori del triangolo di Tartaglia e poi estrae dalle diagonali ascendenti i numeri della successione di Fibonacci.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

class tartfibo
{
  var $tartaglia;
  var $fibonacci;
  var $max;
 
  function tartfibo($max=10)
  {
    $this->max = $max;
    $this->tartaglia = array();
    $this->fibonacci = array();    
    $this->makeTartaglia();
    $this->makeFibonacci();
  }
 
  function makeTartaglia ()
  {
    $this->tartaglia[1][1] = 1;
    $this->tartaglia[2][1] = 1;
    $this->tartaglia[2][2] = 1;
    for($row=3; $row< =$this->max; ++$row) {
      $this->tartaglia[$row][1] = 1;
      for ($col=2; $col< $row; ++$col) {
        $this->tartaglia[$row][$col] = $this->tartaglia[$row-1][$col-1]
                                + $this->tartaglia[$row-1][$col];
      }
      $this->tartaglia[$row][$row] = 1;
    }    
  }
 
  function makeFibonacci ()
  {
    for ($d=1; $d< =$this->max; ++$d) {
      $t = 0;
      for($el=1; $el< =($d+1)/2; ++$el) {
        $t += $this->tartaglia[$d+1-$el][$el];
      }
      $this->fibonacci[$d] = $t;
    }
  }  
}

Demo:

In questa pagina è visibile una demo della classe per n=15.

Download

Il download della classe è disponibile qui.

Conclusioni:

Il triangolo di Tartaglia racchiude nei suoi numeri, diversi piccoli segreti e non è solo un metodo per calcolare i coefficienti binomiali. Provate, per esempio a sommare i numeri di ciascuna riga, partendo dall’alto, danno le potenze di 2. Esistono persino dei frattali! Infine, due grandi matematici, Newton e Pascal hanno rielaborato il suo triangolo per lo studio del calcolo combinatorio. Anche i numeri di Fibonacci, oltre alla relazione con la sezione aurea, hanno implicazioni interessanti, sia con la disposizione geometrica di molte strutture naturali (piante soprattutto) che con l’informatica, per esempio: Fibonacci heap

Riferimenti ed approfondimenti: